ROTATIONAL WORK

ROTATIONAL WORK


1. Work is force times displacement, so for rotation work must be torque times angular displacement:


      

           


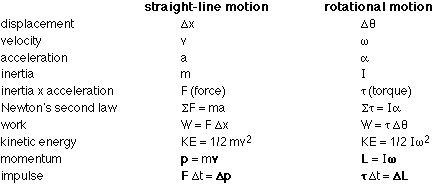
Example 


1. Change revolutions to angle in radians.

     a. 0.5 rev =   3.14 rad  
     b. 5 rev =   31.4 rad 
     c. 3.2 rev =   20.1 rad  

2. When a torque causes a rotation through an angle, the size of the angle can be expressed in degrees or 
     radians  .


3. Work done by a torque is equal to the torque applied times the angle turned through in radians

4.

A flywheel requires 75 ft·lb of work to stop its motion when a braking force of 3 lb is applied at the outer edge. The diameter of the flywheel is 22 in. (Assume that the force is applied tangent to the flywheel or, in other words, that the force is perpendicular to the radius.)A. Find the applied torque in ft·lb. B. Find how many revolutions the flywheel makes as it stops.   Known W = 75 ft·lb F = 3 lb d = 22 in 1 ft = 12 in  1 rev = 2p rad Unknown A) t = ? in ft·lb B) q = ? in rev Equations/Remarks A) L = r = d/2     t = F · L = (F · d)/2     t = (3 lb)(22 in)(1 ft/12 in)/2     t = 2.75 ft·lbB) W = t · q     q = W/t     q = (75 ft·lb)/(2.75 ft·lb)     q = (27.27 rad)(1 rev/2p rad)     q = 4.34 rev

5. A 196 N force is applied to the end of a torque wrench. The arm of the torque wrench is 46 cm long. It causes the wrench to move through an angle of p/4 radians. Find the work done in joules.

  Known

 F = 196 N

L = 46 cm

q = p/4 rad

1 m = 100 cm

1 J = 1 N·m

 Unknown

 W = ? in J

Equations/Remarks

 W = t · q
 t = F · L

t = F · L

W = t · q = F · L · q

W = (196 N)(46 cm)(p/4 rad)(1 m/100 cm)

W = 70.8 J