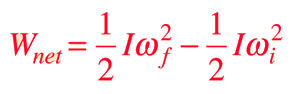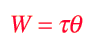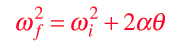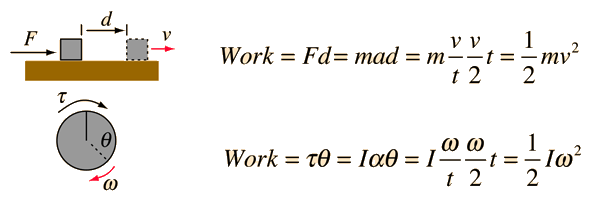1. object of a certain mass moving with particular speed will have an associated kinetic energy
2. An object spinning about an axis will also have associated with it a kinetic energy, composed of the kinetic energies of each individual part of the object.
3These individual contributions may be summed up to give an expression for the total kinetic energy of the spinning object:

3. As with linear motion, where a force did work on an object and led to a change in the object's kinetic energy, for rotational motion the work done by a torque:

4. changing the rotational kinetic energy of an object:

5. Example :
A) Energy is to be stored in a flywheel in the shape of a uniform solid disk with a radius of 1.30 m and a mass of 72.0 kg. To prevent structural failure of the flywheel, the maximum allowed radial acceleration of a point on its rim is 3600 m/s^2.
What I did was solve for the angular velocity through the radial acceleration:
= 3600m/s^2 = rw^2
= w = 52.6 rad/s
Then I solved for the moment of inertia:
I = mr^2 = 72.0kg(1.30m)^2 = 122 kg*m^2
Finally I plugged it all into the rotational kinetic energy equation:
K = (1/2)(122m*m^2)(52.6rad/s)^2
= 1.68*10^5 J
B) A uniform rod of mass 0.20kg and lenght 1.20m is hinged freely about a horizontal axis
through one end of the rod. The rod is raised so that it is horizontal and then released from
the rest so that it rotates about the axis in a vertical plane.
Calculate the
(a) angular velocity
(b) angular acceleration
when the rod makes an angle of 60º to the vertical.
[Moment of inertia of a uniform rod about a perpendicular axis through one end of is 1/3 Ml^2 where M = mass of rod ,l = length]
Example:
a) Calculate the kinetic energy of a rigid body with a mass of 100 kg which is travelling at 20 m/sec.
Solution:
Kinetic energy Ek = (1/2) mv2
Mass = 100 kg and speed = 20 m/sec
= (1/2)(100)(202)
= 20000.
The kinetic energy is expressed in joules
Kinetic energy Ek = 20000 joules.
SOLUTION
a) Using the priciple of conservation of energy,
1/2Iw^2 = mgh
1/2 (1/3 MI^2) w^2 = Mg(1/2 sin 30º )