ROTATIONAL WORK AND KINETIC ENERGY

                

1. MOHD DIN BIN ELSHAL                                                                      54140111069

2.HAMIM SYAKIR BIN SUWARDI                                                            54140111066

3.MUHAMMAD FARHAN BIN MOHD ZAIRY                                        54140111046

4.MOHAMAD NIZAM BIN NOOR MOHAMAD                                       54140111026

ROTATIONAL WORK AND ENERGY

Rotational Work

Work-Energy Principle

The work-energy principle is a general principle which can be applied specifically to rotating objects. For pure rotation, the net work is equal to the change in rotational kinetic energy:

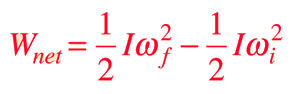
For a constant torque, the work can be expressed as

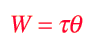
and for a net torque, Newton's 2nd law for rotation gives

Combining this last expression with the work-energy principle gives a useful relationship for describing rotational motion.

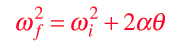
1.

In the picture given above F pulls a box having 4kg mass from point A to B. If the friction constant between surface and box is 0,3; find the work done by F, work done by friction force and work done by resultant force.

Work done by F;

W_F=F.X=20.5=100 joule

Work done by friction force;

W_friction=-F_f.X=-k.mg.X=-0,3.4.10.5=-60 joule

Work done by resultant force;

W_net=F_net.X=(F-F_f).X=(20-0,3.4.10)5

W_net=40 joule

Kinetic Energy

Kinetic energy is the energy of motion. An object that has motion - whether it is vertical or horizontal motion - has kinetic energy. There are many forms of kinetic energy - vibrational (the energy due to vibrational motion), rotational (the energy due to rotational motion), and translational (the energy due to motion from one location to another). To keep matters simple, we will focus upon translational kinetic energy. The amount of translational kinetic energy (from here on, the phrase kinetic energy will refer to translational kinetic energy) that an object has depends upon two variables: the mass (m) of the object and the speed (v) of the object. The 

following equation is used to represent the kinetic energy (KE) of an object

• A rotating body posses kinetic energy, because its constituent particles are moving.
• If the body is rotating with an angular speed w, the tangential speed VT  of a particles at a distance r from the axis is VT = rw
• If the particle's mass is m, it's kinetis energy is 1/2 m(VT)2
• Finally we define KE of rational motion as :  
     
                        

                                                                     

Definition of rational KE:

the rational KE of a girid object rotating with an angular speed w about a fixed axis and having a moment of inertia I.

• Requirement ; w must be expressed in rad/s
• SI Unit ; Joule ( J )

The expressions for rotational and linear kinetic energy can be developed in a parallel mannerfrom the work-energy principle. Consider the following parallel between a constant torque exerted on a flywheel with moment of inertia I and a constant force exerted on a mass m, both starting from rest.

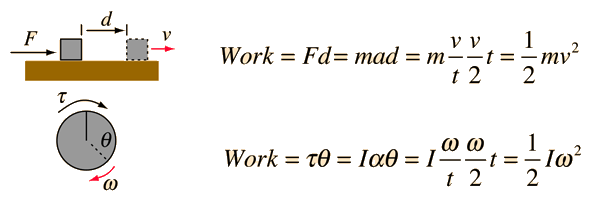
Kinetic Energy of Rolling Object

If an object is rolling without slipping, then its kinetic energy can be expressed as the sum of the translational kinetic energy of its center of mass plus the rotational kinetic energy about the center of mass. The angular velocity is of course related to the linear velocity of the center of mass, so the energy can be expressed in terms of either of them as the problem dictates, such as in the rolling of an object down an incline. Note that the moment of inertia used must be the moment of inertia about the center of mass. If it is known about some other axis, then the parallel axis theorem may be used to obtain the needed moment of inertia.